Kinetic theory: Temperature and kinetic energy

Temperature and kinetic energy

From the ideal gas law

$\displaystyle PV = N k_B T$

(1)

where $\displaystyle k_B$ is the Boltzmann constant, and $\displaystyle T$ the absolute temperature,
and from the above result $P = {Nmv^2\over 3V}$ we have $PV = {Nmv_{rms}^2 \over 3}$
we have $\displaystyle N k_B T = \frac {N m v_{rms}^2} {3}$
then the temperature $\displaystyle T$ takes the form

$\displaystyle T = \frac {m v_{rms}^2} {3 k_B}$

(2)

which leads to the expression of the kinetic energy of a molecule

$\displaystyle \frac {1} {2} mv_{rms}^2 = \frac {3} {2} k_B T.$

The kinetic energy of the system is N times that of a molecule $K= \frac {1} {2} N m v_{rms}^2$
The temperature becomes

$\displaystyle T = \frac {2} {3} \frac {K} {N k_B}.$

(3)

Eq.(3)₁ is one important result of the kinetic theory: The average molecular kinetic energy is proportional to the absolute temperature. From Eq.(1) and Eq.(3)₁, we have

$\displaystyle PV = \frac {2} {3} K.$

(4)

Thus, the product of pressure and volume per mole is proportional to the average (translational) molecular kinetic energy.
Eq.(1) and Eq.(4) are called the "classical results", which could also be derived from statistical mechanics; for more details, see .^[1]
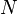Since there are $\displaystyle 3N$ degrees of freedom in a monoatomic-gas system with $\displaystyle N$ particles, the kinetic energy per degree of freedom is

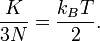
$\displaystyle \frac {K} {3 N} = \frac {k_B T} {2}.$

(5)

In the kinetic energy per degree of freedom, the constant of proportionality of temperature is 1/2 times Boltzmann constant. In addition to this, the temperature will decrease when the pressure drops to a certain point. This result is related to the equipartition theorem.
As noted in the article on heat capacity, diatomic gases should have 7 degrees of freedom, but the lighter gases act as if they have only 5.
Thus the kinetic energy per kelvin (monatomic ideal gas) is:

per mole: 12.47 J
per molecule: 20.7 yJ = 129 μeV.

At standard temperature (273.15 K), we get:

per mole: 3406 J
per molecule: 5.65 zJ = 35.2 meV.

Kinetic theory

Wednesday, 6 July 2011

Temperature and kinetic energy

Temperature and kinetic energy

No comments:

Post a Comment